2y To The Third Power

Lesson 2: Exponents

/en/algebra-topics/social club-of-operations/content/

What are exponents?

Exponents are numbers that take been multiplied by themselves. For instance, iii · 3 · iii · 3 could be written as the exponent 3^four : the number 3 has been multiplied by itself 4 times.

Exponents are useful because they let us write long numbers in a shortened course. For instance, this number is very large:

1,000,000,000,000,000,000

But you could write information technology this mode as an exponent:

x^eighteen

It too works for small numbers with many decimal places. For instance, this number is very small only has many digits:

.00000000000000001

It also could exist written every bit an exponent:

10^-17

Scientists oftentimes apply exponents to convey very large numbers and very small ones. You'll see them often in algebra problems too.

Agreement exponents

Equally y'all saw in the video, exponents are written like this: iv^three (you lot'd read it every bit 4 to the tertiary power). All exponents have ii parts: the base, which is the number being multiplied; and the power, which is the number of times you multiply the base.

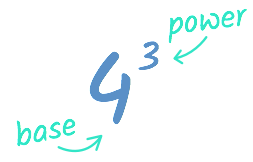
4 to the third power

Because our base of operations is 4 and our power is 3, we'll demand to multiply 4 past itself three times.

4³ = 4 ⋅ four ⋅ 4 = 64

Because 4 · iv · 4 is 64, 4³ is equal to 64, too.

Occasionally, y'all might encounter the same exponent written like this: five^3. Don't worry, it's exactly the same number—the base is the number to the left, and the ability is the number to the right. Depending on the type of computer you use—and especially if you're using the computer on your telephone or computer—you may demand to input the exponent this fashion to calculate it.

Exponents to the 1st and 0th power

How would you simplify these exponents?

seven^one 7⁰

Don't experience bad if you're confused. Even if you feel comfortable with other exponents, it'south non obvious how to calculate ones with powers of 1 and 0. Luckily, these exponents follow unproblematic rules:

Exponents with a power of 1
Any exponent with a power of one equals the base, then 5^one is 5, 7¹ is 7, and x^one is x .
Exponents with a power of 0
Whatever exponent with a power of 0 equals one, so 5⁰ is i, and and so is seven⁰, x⁰, and any other exponent with a ability of 0 you can call back of.

Operations with exponents

How would you solve this problem?

2ⁱⁱ ⋅ ii³

If y'all think you should solve the exponents first, then multiply the resulting numbers, you're right. (If you weren't sure, bank check out our lesson on the order of operations).

How about this one?

10³ / x²

Or this one?

2x² + 2x^two

While you can't exactly solve these problems without more information, y'all tin simplify them. In algebra, you volition oft be asked to perform calculations on exponents with variables as the base of operations. Fortunately, it's easy to add, subtract, multiply, and carve up these exponents.

Adding exponents

When you're adding two exponents, yous don't add together the actual powers—you add the bases. For example, to simplify this expression, you would but add together the variables. You accept two xs, which can be written as 2x. So, 10²+10ⁱⁱ would exist 2x² .

10 ² + x ² = 2x^two

How about this expression?

3y^four + 2y⁴

You're adding 3y to 2y. Since iii + 2 is 5, that means that 3y^iv + 2y⁴ = 5y^four .

3y ⁴ + 2y ⁴ = 5y^iv

Yous might take noticed that nosotros only looked at issues where the exponents we were adding had the aforementioned variable and power. This is considering you tin merely add together exponents if their bases and exponents are exactly the same. So you can add together these below because both terms accept the same variable (r) and the aforementioned power (seven):

fourr⁷ + 9r⁷

You can never add together any of these as they're written. This expression has variables with two different powers:

4r ³ + 9r ^eight

This one has the same powers merely dissimilar variables, so you can't add it either:

4r ² + 9s ²

Subtracting exponents

Subtracting exponents works the aforementioned as calculation them. For example, can you figure out how to simplify this expression?

5x² - 4xⁱⁱ

v-four is 1, so if you lot said 110 ^two , or simply x ^two , you're correct. Recall, but like with adding exponents, you lot can only subtract exponents with the same ability and base.

vx² - 4xⁱⁱ = 10²

Multiplying exponents

Multiplying exponents is simple, just the mode y'all do it might surprise you. To multiply exponents, add the powers. For instance, take this expression:

x^three ⋅ x⁴

The powers are 3 and four. Because 3 + 4 is seven, we can simplify this expression to x⁷ .

ten ³ ⋅ x ⁴ = 10⁷

What about this expression?

3x² ⋅ 2x⁶

The powers are ii and vi, and so our simplified exponent will accept a ability of 8. In this case, nosotros'll also need to multiply the coefficients. The coefficients are 3 and ii. We need to multiply these like we would whatsoever other numbers. three⋅2 is six, so our simplified reply is 6x^eight .

3x² ⋅ 2x⁶ = 6x⁸

You tin can only simplify multiplied exponents with the same variable. For example, the expression 3x²⋅2x^three⋅4y ² would exist simplified to 24x⁵⋅y ². For more data, go to our Simplifying Expressions lesson.

Dividing exponents

Dividing exponents is similar to multiplying them. Instead of calculation the powers, you subtract them. Take this expression:

x^viii / x²

Because 8 - 2 is 6, we know that 10⁸/10² is 10^half-dozen .

x ⁸ / ten ² = x⁶

What about this i?

10x⁴ / 2x²

If you think the reply is 5xⁱⁱ , you're right! 10 / 2 gives us a coefficient of 5, and subtracting the powers (4 - 2) ways the power is two.

Raising a ability to a ability

Sometimes yous might see an equation similar this:

(10^five)³

An exponent on another exponent might seem confusing at first, but you already have all the skills you lot need to simplify this expression. Call back, an exponent means that y'all're multiplying the base of operations by itself that many times. For example, 2³ is 2⋅two⋅ii. That ways, we can rewrite (x^v)ⁱⁱⁱ as:

ten⁵⋅x⁵⋅x^five

To multiply exponents with the same base of operations, but add the exponents. Therefore, x^v⋅x^five⋅x⁵= ten⁵⁺⁵⁺⁵= x¹⁵.

There'southward really an even shorter way to simplify expressions similar this. Take another expect at this equation:

(ten^five)³= x¹⁵

Did you observe that five⋅three as well equals 15? Think, multiplication is the same equally adding something more than one time. That ways we can think of v+5+5, which is what we did earlier, as 5 times 3. Therefore, when you heighten a ability to a power you tin can multiply the exponents.

Let'due south wait at ane more instance:

(x^half-dozen)^four

Since 6⋅4 = 24, (x⁶)⁴= x²⁴

x²⁴

Let'southward look at one more example:

(3x⁸)⁴

Get-go, nosotros can rewrite this equally:

3x⁸⋅3x^viii⋅3x^eight⋅3x⁸

Call back in multiplication, lodge does non thing. Therefore, we can rewrite this once more equally:

3⋅3⋅iii⋅iii⋅x^eight⋅x⁸⋅x⁸⋅x⁸

Since 3⋅3⋅3⋅3 = 81 and x⁸⋅10⁸⋅10⁸⋅ten⁸= x³², our respond is:

81x³²

Observe this would have also been the aforementioned as 3^four⋅ten³² .

Still confused about multiplying, dividing, or raising exponents to a ability? Check out the video beneath to learn a fob for remembering the rules:

/en/algebra-topics/negative-numbers/content/